Math for the People

Section 1.6 Quantifiers

A quantifier is a way of indicating quantity within a statement. We know words that indicate quantity such as all, many, some, or none. In logic, these are the words that are used as the quantifiers. They indicate how many of what have a particular attribute or quality. Consider the following examples:

1. Some abortions are medically necessary.

2. All children deserve to live.

3. No abortion supporter deserves a vacation.

One important tool that supports us when working with statements with quantifiers is the use of Venn Diagrams and set representations. Sets help us have a more clear perspective in forming negations and understanding the truth value of statements. Let’s start with the simple statements that use quantities, and then build to a more complicated statement like the one from the previous section, "If abortions are not a federally protected right, then no one will get an abortion."

Let's consider the statement that some abortions are medically necessary. The word some is a quantifier. The reference set is the set of all abortions. The set of abortions for medical reasons is what we would consider a subset. Exploring the legitimacy of this subset is how we decide on strategies for negation. Our main strategy is driven by determining if there are abortions in the subset "abortions for medical reasons." A quick web search can help us determine if there are abortions for medical reasons (see https://www.health.com/news/abortion-medically-necessary¹ as an example), meaning that the set of abortions for medical reasons is not an empty set. This web article discusses that the medical reason may be for both the mother or the unborn fetus. We can use our understanding of the characteristics and membership of the sets to help us think further when working with statements about the sets.

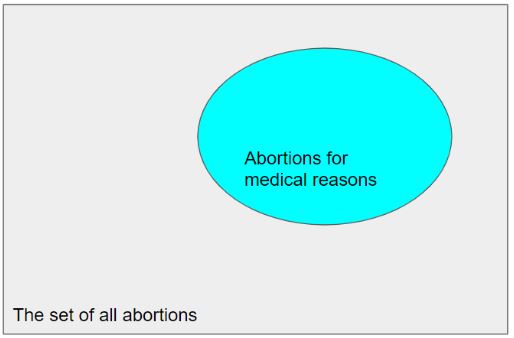
We can use the membership of the set and subset to help develop strategies for negating statements. As previously stated, negations switch the truth value of a statement. This would also be true for quantified statements, except the change happens by altering the quantity. We established previously that the statement "Some abortions are medically necessary," is a true statement. So we need to think about ways to use quantity and set membership to change the truth value. In this case, our negation would be to find a false statement. Since we know that some abortions are for medical reasons, the most direct negation is to claim that no abortions are medically necessary. We know that this statement is false, as we can produce information about abortions that are medically necessary for the safety of the mother. The statement, "No abortions are medically necessary," would propose that there is not an element in the set abortions for medical reasons.This switches the truth value from the original statement, "Some abortions are medically necessary."

One question that you may have is why the statement, "All abortions are medically necessary," is not a valid negation. It may in fact be a valid negation, but we have to meet some specific criteria for it to be valid. Let’s talk about what needs to happen for the negation with "All abortions are medically necessary," to be valid. The statement implies that all of the abortions in the set of all abortions are also in the set of abortions for medical reasons. Now let's consider our original statement, "Some abortions are medically necessary." It is logically equivalent to the statement, "Not all abortions are medically necessary." The negation of this equivalent statement happens when we state that there are no members in the set of all abortions that are not also in the set of abortions for medical reasons. This is a more complicated process because it is not direct. We created an equivalent statement that was then negated. Typically the more steps that are involved in a process, the more room you have to make errors. Logic is no exception.

Let's now consider the statement, "All children deserve to live." This is a common quantified statement that is offered in abortion debates. Let's discuss the sets, and think independently about potential subsets that can exist.

So, let's take some time to consider this set image. We know that the set of children that deserve to live is a subset of the set of all children. Our goal is to think about if there are any subsets or groups of children that should be excluded from the set of children that deserve to live, but would still be considered part of the set of all children. As an author, I have contemplated the question of if these sets were different for quite a long time, and I continue to come to the conclusion that the sets are the same.

This equivalence of sets helps give us a strategy for negation. We know that every child is in both the set of all children and the set of children that deserve to live. If we can find a single child that does not belong in the set of children that deserve to live but still belongs to the set of all children, then we can negate the statement with the claim, "At least one child does not deserve to live." It seriously only takes one to negate the statement, but we know that case is not likely to exist. Another equivalent statement that is an option for a negation is the statement, "Some children do not deserve to live." These two statements both claim that there are children that do not belong in the set of children that deserve to live.

Now, let's consider the statement, "No abortion supporter deserves a vacation." This claim is a bit more complex, so let's start with our sets. We will lay out the sets the way that they are proposed in the statement.

Notice that there is no overlap shown between the set of people that deserve vacations and the set of people that support abortions. We are starting with a diagram that matches the original claim of the statement. We use this to establish the initial truth value of the statement. Vacations tend to be labeled as something that is a privilege, but really vacations are just a break from work or school (https://www.merriam-webster.com/dictionary/vacation). It appears that everyone deserves a vacation, so the set of all people and the set of people that deserve a vacation are equivalent sets. We also know that people that support abortion are people, who would also need a vacation. This means that the initial claim is false. Let’s think about strategies to work with the statement, so that we can approach negation. Our first step would be to update the set diagram.

The most clear path to a negation, which in this case is the creation of a true statement, is to use the set diagram to generate a statement. In this case it will take the form of a statement about all people that support abortion. The statement, “All abortion supporters deserve a vacation.” would be a negation of the original statement, "No abortion supporter deserves a vacation."

A more complicated version of a quantified statement is the statement, "If abortions are not federally protected, then no one will get an abortion." This statement is more complicated because of the fact it is a conditional statement. When there is a conditional statement and a quantifier, we can think about combining the diagrams for two separate sets. The first set is related to the condition, and it is split between "Abortion is federally protected," and "Abortion is not federally protected." The set diagram provides the following base.

Now we have a secondary set to think about: people getting abortions. The question that we have to ask ourselves becomes: Will abortions still happen if abortions are not federally protected? In prior sections, we discussed that some abortions are medically necessary. There are also (while often dramatized for television, like Law and Order: SVU (see Season 12, Episode 9: “Gray” as a specific example) scenarios where one partner in a couple will go to desperate lengths to terminate a pregnancy. A medication is administered to terminate the pregnancy. One issue that was debated during the episode was if the action of the partner was technically an abortion. The court determined that it met the legal definition of an abortion because medical means were used to terminate a pregnancy. We use this example, not only because it is widely available via the internet, but to demonstrate that abortion does not require a medical practitioner. This means that even without clinics and medical practitioners, abortions will still happen. This means that overlaying the second set gives us a diagram that looks something like the set diagram below.

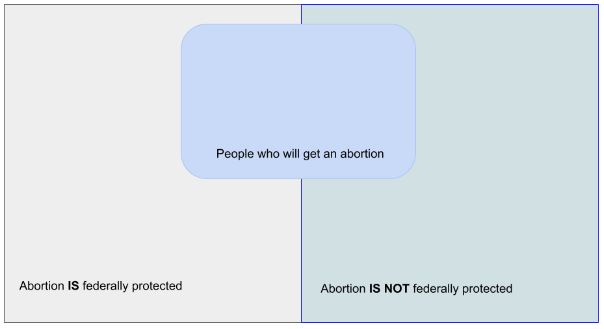
We can see that the set of people who will get an abortion is evenly split over the two scenarios of abortion being federally protected or not being federally protected. This means that when we think about the original statement, “If abortions are not federally protected, then no one will get an abortion,” we can see that this is a false statement as long as the set of people who will get an abortion is not an empty set. We have strong reason to believe that this set is not empty, both from the example from the Law and Order example as well as the case of medical abortions mentioned previously.